Differentiation is a topic often encountered in senior level calculus at high school. While some people find it an easy topic to grasp, others struggle with the various rules and methods introduced when first differentiating an equation.

To keep this article short and sweet, I’ll assume some previous knowledge of derivatives. Here, I’ll take you through a quick and hopefully easier way to differentiate almost any real algebraic equation with respect to one independent variable.

Step 1: Start from the outside and work your way in

The first step is to take the derivative of each term, starting from the outer most terms and working your way in. This is like applying the “chain rule” and differentiating each term with respect to the independent variable, x. I like to call this the “rainbow method,” as the arrows form a rainbow-like schematic on the terms that you should apply the differential to.

I apologise for jumping into a slightly complicated example straight off the bat, but I wanted to show that this method really works!

Step 2: Differentiate using conventional rules

While we still have to use the conventional “product” and “chain” rules (note that the “product” rule can be used in place of the “quotient” rule using indices), we have managed to avoid using dummy variables in our previous step. I find that dummy variables (e.g. u and v) make the entire process more confusing. Thus, to the first term I have applied the “chain” rule and to the second term I have applied the “product rule.” I’ve colour coded them to identify the rule that was applied to each term.

Which gives:

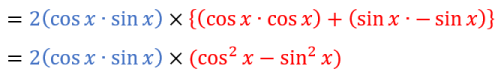
Simplifying the above results in:

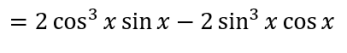
And there you have it, your final answer! The above can be further simplified to
1/2sin(4x) by tinkering around with trig identities, but I won’t delve into that here. Now, let’s try a more difficult example…

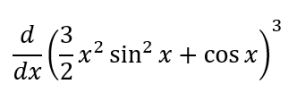
As before, we apply the “rainbow” method to each term:

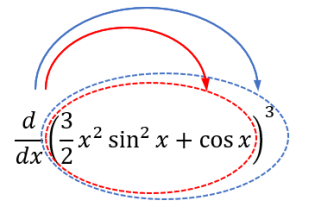
While at first we differentiate each term on a macro scale, we actually need to go deeper and apply the d/dx to the cos(x) function as well, however, the cos(x) still remains within the argument inside the brackets. This is shown schematically as:

Now we differentiate using some of the conventional rules we used previously. We apply the “chain” rule to the overall equation, the “product” rule to the 3/2 x^2 sin^2(x) term and trig rules to differentiate the cos(x) term.

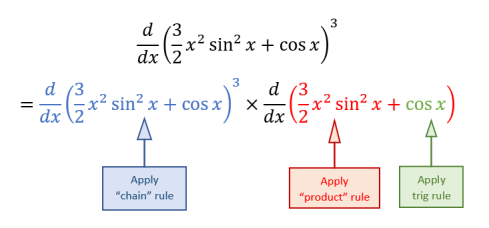
This results in:

Note that we have applied the “chain” rule to differentiate sin^2(x). This could also be evaluated using the “product” rule and re-writing as d/dx (sin(x)*sin(x)). Try it yourself, you should get the same result of: 2sin(x)cos(x).

Removing the clunky brackets gives us a final answer of:

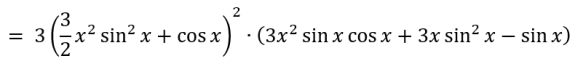
Confirming with Wolfram Alpha…yep! It checks out!

A lot of these problems may require a fair bit of practise to master, but once you’ve tried this method of differentiation on various equations, you’ll find that it becomes second nature, and saves a lot of writing space and time. I hope this method helps you strengthen your skills in differentiation. If you have any feedback or recommendations, feel free to leave a comment below and I will be sure to check it out.